Terraformering
2002-07-12Fn diskuteras hur sjukdomar och ändrade civilisatoriska processer leder till att befolkningsökningen motverkas. I den rika världen, i Europa diskuteras om hur välutbildade kvinnor föder få eller inga barn. Både katastroferna i 3je världen och dessa skeenden i den rika världen bör inte överskyla det faktum att en ökande befolkning leder till problem och att det när som helst kan komma att aktualiseras. Den här sortens varningar kom för hundratals år sen men farhågorna besannades ju inte eller?
De som förlorade anhöriga under det första världskriget kanske inte satte det i samband med befolkningsökning, men det går inte att komma ifrån att det och andra krig har att göra med konkurrens om begränsade resurser antingen det gäller land eller råvaror.
Man behöver bara ta en promenad i svenska marker för att stöta på problemet med att stränder är delvis blockerade från allmän användning genom att folk har strandtomter. Detta trots att det finns strandskyddsregler och trots att vi är jämförelsevis glest befolkade. I det här sammanhanget är jag inte ute efter att diskutera strandskydd specifikt utan jag menar bara att det är en påminnelse om att vi har ändliga resurser och ju fler vi blir desto fler potentiella konflikter.
En exponentiell befolkningstillväxt går inte att hantera med några kända tekniska finurligheter. Naturlagarna sätter stopp för det. Antingen måste det finna ngn process som avlivar oss med nära samma intensitet så att det nettomässigt inte blir en exponentiell tillväxt eller också måste födelsetalet minska.
Det hjälper inte ens att flytta ut i rymden om befolkningstillväxten är exponentiell.
En långsammare befolkningstillväxt kan däremot vidmakthållas förutsatt att man är beredd att uthålligt bemöda sig om att lösa de problem som uppstår med alla tillgängliga metoder.
Nu tänkte jag diskutera vad man kan göra för att öka tillgänglig mark här på jorden. Vad finns det för möjligheter att göra jorden större?
Om man tänker sig att man bara skulle hämta hit materia utifrån och smäcka på efter hand så skulle jordens storlek öka till att börja med men även dess gravitation. Det är antagligen inte ngn attraktiv lösning eftersom gravitationen på ett känsligt sätt griper in i det levandes villkor.
Emellertid är det möjligt att öka jordens storlek med bibehållen gravitation genom att man successivt byter ut tyngre materia i jordens innandöme mot lättare materia som fyller ut.
Tätheten i jordens innandöme i den tunga kärnan lär ligga grovt sett kring 10 gr/cm3.
Och tätheten hos vanligt berg är kanske 3 i samma enheter. Om vi tänker oss att man under lång tid och under väl kontrollerade betingelser skulle genomföra att tätheten ändrades till ett lägre värde samtidigt som storleken ökade med hela tiden bibehållen gravitation vid ytan kan den motsvarande storleksordningen beräknas. I appendix är utgångspunkten att kärnan skall ha samma täthet som manteln som där uppskattas, i utgångsläget, till i medel 4.7 (ej noga) och där erhålls uppskattningen att radien kommer att kunna öka med 33% (ej noga)
Motsvarande ökning av area: 1.332~1.77 dvs 77 % ökning av arean.
Om man ändå hämtar mkt materia utifrån kan man antagligen även hämta mer vatten om det är önskvärt. Emellertid förefaller det mer sannolikt att man inte vill det utan att det bara är den övre delen av havet som är fotosyntetiskt aktiv som man egentligen ’behöver’.
Så det vatten som finns idag kanske räcker gott och väl för en sådan större jord.
När jorden har större radie förändras förhållandena för atmosfären också. Jag ger mig inte in på ngn beräkning, men det behövs om man skall få en klar bild av vilka begränsningar som gäller. Om ingen speciell åtgärd vidtas förefaller det rimligt att en tyngre atmosfär skulle kunna hållas på plats. Det är vi inte vana vid. Min gissning är att en sån atmosfär erbjuder större möjligheter för liv än den gamla.
(Högre tryck och andra förändringar av atmosfären leder antagligen till problem för metabolismen och antagligen skulle det krävas motsvarande förändringar i arvsmassan. Det är inte säkert att det skulle gå att justera atmosfärens sammansättning ens om man visste exakt vad man ville uppnå. För det kanske inte finns ngn balans som precis passar in på livets villkor i sin tidigare form. Men om man tänker sig att förändringen sker långsamt borde det finnas goda möjligheter att lämplig sammansättning av arvsmassan hinner ’provas ut’. Även om förändringen skulle inträffa helt utan några människor närvarande.)
Det blir lättare att flyga så större flygande varelser blir möjliga. Solljuset förändrar karaktär. Det kanske knappt syns solnedgångar och färgen blir rödare redan för vinklar närmare zenit. Jag tror att själva himlen blir blåare. Det är tänkbart att det blir rätt färgsprakande. Men jag vet inte hur stor effekten blir eftersom jag inte försökt räkna på det.
|
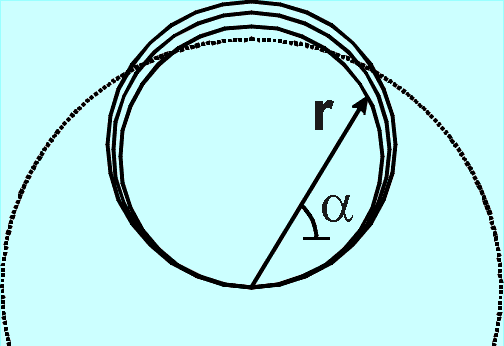
Med en tätare och samtidigt djupare atmosfär kommer dessutom ljuset att böja av så att man i princip kan se runt horisonten. Den sortens optiska förhållanden undersöktes teoretiskt av James Clerk Maxwell på 1800-talet. Om man tänker sig att tätheten är hög och varierar med radien rör sig ljuset längs krökta banor i stället för rätlinjigt. Man kan räkna fram att om brytningsindex varierar som n=1/r1+m inom en del av atmosfären så rör sig ljuset i enlighet med samband av typen rm=sin(ma) där r, a är avstånd och vinkel, (se figur). Maxwells fall motsvarar, om jag minns rätt, n=1/r2, och det motsvarar att ljuset rör sig längs cirkelbågar där den tänkta fortsättningen passerar genom jordens centrum. Om Maxwells fall existerade fullt ut i verkligheten skulle man kunna se sig själv i nacken i skala 1:1 trots att ljuset passerat en sträcka av pRJ där RJ är jordradien dvs en sträcka av ca 20000 km. Den sträckan i vakum skulle ge en fördröjning av 0.07 sekunder. Men vore det vakum skulle det ju inte bli en krökt bana. Om det fanns en verklig situation med ett sådant brytningsindex skulle fördröjningen bli oändlig, pga av den stora förtätningen i centrum. Men om man tänker sig en liten avvikelse från det givna sambandet så att det var ändlig brytning i ett mindre område kring centrum, skulle fördröjningen bli mer hanterlig, och beroende på hur man valde avvikelsen från den ursprungliga formeln skulle man kunna få olika fördröjningar. Vitsen med att diskutera såna exotiska situationer är för mig inte att det verkar nyttigt utan snarare att det kontrasterar mot vår vardagserfarenhet. Om man ofta såg sig själv utifrån med fördröjning, men inte var riktigt säker på vem man såg hur skulle man påverkas av det?.
Beträffande den verkliga situationen i det modifierade jordklotet. Det är inte säkert att den verkliga effekten blir så stor under de kvantitativa förhållanden som föreslogs ovan. Om beroendet är n=1/r blir sambandet en spiral r=eka där k beror av ljusets startriktning. Om startriktningen är nära tangentiell vindlar spiralen långsamt. Även om atmosfärens egenskaper vore sådan att det gav upphov till starka brytningseffekter finns det andra inskränkande faktorer. Det finns samband mellan ljusbrytning och absorption som ger begränsningar för i hur hög grad dessa tänkta förhållanden kan realiseras. Det vi benämner kausalitet, dvs orsaks/verkan-samband kan bl a uttryckas som ett bindande samband mellan ljusbrytning och absorption vilket man kanske inte skulle vänta sig vid första påseendet. Det innebär att absorptionen antagligen skulle ta överhanden innan det blev riktigt extremt. Dvs antagligen skulle det aldrig bli så intressant att man kunde se sig själv bakifrån t ex. Absorptionen skulle antagligen göra det mindre intressant och effekten skulle bli mkt mer måttlig. Uppdatering 2002-08-21Det var nog följande fall jag egentligen var ute efter. Jag har inte orkat kolla Maxwells samlade verk, men jag har bestämt för mig att det var det här fallet. I ett medium med brytningsindex n(r)=n0/(1+r2/C2) rör sig ljuset i cirkelformiga banor som ej passerar genom centrum. Låt dessa cirklar ha radie B och centrum på avståndet A från r=0. A och B uppfyller då sambandet B2-A2=C2 Beroende på i vilken riktning en ljusstråle sänds ut från början så kommer den att fortsätta runt ngn av cirklarna som definieras av det sambandet. |
Med en atmosfär som lättare tillåter varelser att flyga skulle det säkert också i motsvarande grad bli en massa stoft som drev omkring i atmosfären kanske så mkt att det skulle bli ett allvarligt problem om skillnaden blev stor jmf med den vanliga jorden, där det redan finns massor av skräp i luften.
Antagligen ligger vi inte så lång ifrån optimum, men kanske lagom långt ifrån för att det skall finnas en viss mån för förbättringar som åtminstone kan intressera den vetenskapligt nyfikne.
Men detta med såna krökta signalbanor kanske skulle kunna ha en tillämpningen i den mikroskopiska världen i stället. Man vet aldrig vad som händer om man söker omtolka atomära fenomen, utan att komma i konflikt med kända fakta. Det är emellertid en annan historia.
I varje fall ger det uppslag till hur en optimal planet skulle kunna utformas om man strävade efter att få en annan typ av evolution.
(Oavsett om man tror att det finns en intelligent skapande kraft bakom alltsammans från början eller inte så tvingas man ju i vilket fall som helst att spela den rollen själv när man funderar i såna banor.)
Om man släpper kravet på att gravitationen skall vara precis som vår nuvarande och även tänker sig att bygga planeten av ngt mer lättviktigt material blir det möjligt att få måttlig tyngdkraft samtidigt med tät atmosfär. Om man tänker sig att det därvid skulle bli för varmt pga av växthuseffekt så får vi föreställa oss att man motverkar det på lämpligt sätt. Ett radikalt sätt är att som jag beskrivit i ett annat dokument blockera bort en del av solljuset med skärmar i rymden.
I en sån värld går det mkt lättare att flyga av egen kraft och den biosfären bleve nog full av drakar.
Det kanske är potentiella världar av det slaget som kommer till människan i hennes litterära fantasier och folktro.

Tillbaka till Introduktion
Appendix - formler
K1=4p/3 1)M1= K1 [q1R13+ q0 (R03-R13)] g1=GM1/R02 2)M2= K1 [q0R0’3] g2=GM2/ R0’2 g1=g2 => [q1R13+ q0(R03-R13)]/R02= q0R0’ Potentiell energi W2/W1= R0´/R0 R0’/R0=1+(q1/q0 - 1)(R1/R0)3 N=(R1/R0)3 R1~3.47*106 R0~6.37*106 <q>= q1N+ q0(1-N) <q>~5.5*103 N=0.156, q1~104 => q0~4.67*103 (ej noga) R0’/R0=1+(10/4.67 - 1)0.156 ~ 1.33 (samma ökning av potentiell energi) | |||||||||||||||||||||||||||||