Lens Windows for Underwater Photography: The Flat Glass Sheet and the Dome Port
Most underwater photographers know what a dome port is: a spherical window applied on underwater camera housings for wide-angle lenses. What many do not know, is how it works, with advantages and disadvantages etc.. Some photographers also think, that the dome port is the only solution for all types of lenses. Here in this article the matter is clarified.
The dome port is today the established "lens window" for housed cameras with wide- angle lenses. This was however not the case in the early days of underwater photography. Then the natural choice was a flat glass sheet. It was not until the beginning of the seventies, that the dome port became known and accepted, very much thanks to an article that appeared in Skin Diver in October 1970, see ref. [1]. Below I will explain both how the flat glass sheet acts and how the dome port acts at underwater photography. Both are used today, but in connection with different types of lenses.
A flat glass sheet
An aquarium is normally built from flat glass sheets. You have probably many times looked into an aquarium. You have perhaps also taken photographs through its glass walls. A striking effect in this situation, is the strong refraction of light. The effect is more evident if your angle of view deviates from perpendicular. If you move your head this effect could make you almost dizzy. Having experienced this situation, it is easy to question the suitability of a flat glass sheet as an underwater photographic window, especially for wide-angle lenses. In practice a flat glass sheet works well for lenses with small angles of view, such as "standard" lenses and telephoto lenses. Today the flat lens port is used for macro-lenses, which normally have angles of view between 40o and 30o. For angles around 60o, the flat lens port starts to produce poor results, and it becomes unacceptable for angles above 75o.
|
Figure 1 |
|
|

|
This is a reference picture of a the testchart taken "above water"
Lens: Sigma 2.8/28
Aperture: 4
The testchart consists of six "cards". The bigger "card" to the right is the lower right corner "card" enlarged. |
|
Figure 2 |
|
|

|
This is a picture of the same testchart taken under water
Lens: Sigma 2.8/28
Aperture: 4
Window: Flat
The pincushion-shaped distortion is clearly visible, also mark the decreased resolution at corners |
Figure 2 above shows the result having a flat glass sheet together with a 2.8/28 (35mm format) wide-angle lens. This lens has an angle of view of around 75o. If you compare with the reference picture in figure 1, you can see, that the resolution in the corners has decreased, and a barrel-shaped distortion has been introduced. The distortion is inevitable, which is also the case with decreased resolution, and both are worsened with increasing angle of view. The decreased resolution is caused by chromatic aberration, which is accompanying the flat glass sheet. Both these effects can be watched in the aquarium: blame the chromatic aberration for details with rainbow-colored edges; put down a paper with a square printed on it to see the barrel-shaped distortion. Also another phenomenon can be seen in the aquarium: a magnifying effect. This leads to a decreased angle of view. The amount of this decrease can be seen in table 1. It is of course very undesirable to get a reduction of the angle of view for a wide- angle lens, whereas it could be an advantage for a macro lens.
|
Table 1
Reduction of diagonal angle of view with flat glass port |
|
Focal length [mm] |
Diagonal angle of
view in air [ o] |
Diagonal angle of
view underwater [ o] |
|
35 mm format
(24x36) |
Medium format
(6x4.5) |
|
50 |
80 |
45 |
33 |
|
35 |
55 |
61 |
45 |
|
28 |
45 |
75 |
53 |
|
24 |
- |
84 |
59 |
|
20 |
35 |
94 |
66 |
|
15 |
24 |
180 |
Impossible to combine fisheye with flat port ! |
If you compare the "air" values with the "underwater" values, you can see that a 20 mm lens is "reduced" to a 35 mm focal length lens, if you use a flat glass port. On the other hand, this effect also leads to an increased distance between object and lens (for the same size of the object in the finished picture), which can be desirable photographing delicate and/or shy marine animals. An accompanying effect is, that real object to lens distances are reduced to virtual values of around 3/4 (of the real). Everyone who has used a diving mask knows about this.
The dome port
The dome used as an underwater lens port, causes, in contrast to the flat port, little degradation of the "in air" properties of the lens. The angle of view is maintained and distortion and chromatic aberration are negligible. Maintaining the angle of view is especially important for wide-angle lenses, as the purpose with the wide-angle lens is to get as close as possible to the subject, because of the limited visibility. The dome port has however also negative properties. The most prominent is named "curvature of field". What is curved is the virtual picture of the object. The dome is creating a curved virtual picture of a flat object. This is accompanied by a reduction of distance. The curved virtual picture is situated at a considerably smaller distance than the actual. For an actual lens to object distance of 3 m, the reduced distance is typically 0.3 m. Lets first discuss the reduction of distance and after that the curvature of field.
Reduction of distance
As the virtual picture is situated at a considerably smaller distance than the actual, it is necessary to focus the lens on this smaller distance. The focusing range of a lens is however limited, typical smallest focusing distance of a super wide-angle lens is around 0.3m. Often this is not enough to take care of a desirable focusing range; for far-away subjects at distances larger than 3m it will work, but not for subjects at for instance actual distance of 0.5m. One solution on this problem is a close-up lens of suitable strength. The dome in figure 3 below requires for instance a close-up lens of strength +3 diopters. Such close-up lenses are however degrading the optical performance of the lens, and for extreme wide-angle lenses it becomes more and more difficult because of vignetting. For fisheye lenses with an angle of view of 180o a close-up lens is of course physically impossible.
The best solution
Another solution (better, but more complicated to achieve) is a thin extension ring. It is normally not possible to use standard extension rings, as they are too thick. Often it is however possible to achieve the desired small extension by putting shims into the lens mount. Typical extensions for super wide-angle lenses are in the range 0.8mm to 2.5mm.
The most practical solution
As the most practical solution is a close-up lens, suitable strength of such lenses are given in table 2 below. The strength is dependent on the dome radius according to the table. It is often difficult to find close-up lenses with diopter numbers other than 2, 3 and 4. Some manufacturers can provide lenses also with "half" numbers, and somtimes also "quarter" numbers. The most commonly used domes have radii around 90 mm, suitable for +3 close-up lenses.
|
Table 2.
The calculated diopter values below are based on the assumptions of a thickness/radius ratio of 0.066666, and ocean water |
|
Outer surface radius of dome, mm |
Strength of close-up lens, diopters, + |
|
50 |
5.52 |
|
55.20 |
5.00 |
|
65 |
4.25 |
|
69.13 |
4.00 |
|
73.76 |
3.75 |
|
79.01 |
3.50 |
|
85 |
3.25 |
|
92.21 |
3.00 |
|
100.58 |
2.75 |
|
110.65 |
2.50 |
|
123.01 |
2.25 |
|
138.43 |
2.00 |
|
150 |
1.85 |
Curvature of field
Figure 3 below shows how the curvature of field looks for different lens to object distances. It is the result of an optical analysis of a dome port with outer radius 90mm and thickness 7mm in ocean water.
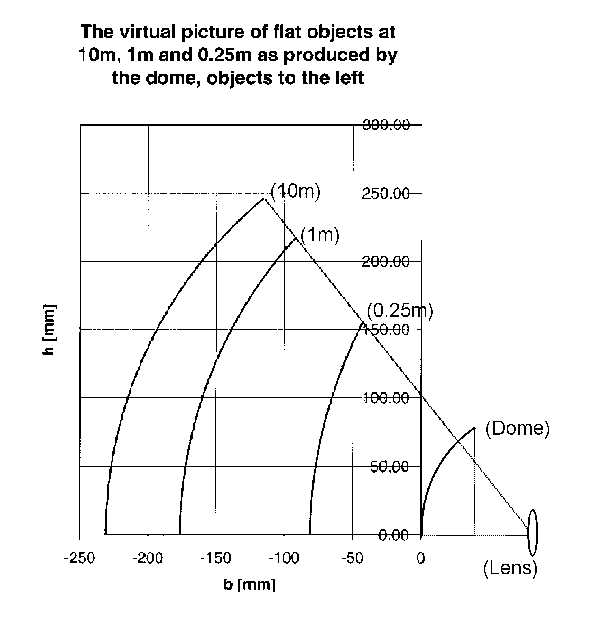
Figure 3.
b is the distance from the dome to the virtual picture, in mm, h is the distance from the optical axis, in mm. The curvature is of course symmetric about the optical axis.
Figure 3 shows, that the curvature of field is smaller for smaller distances. For a lens to object distance of 10m, the curvature is almost identical to a circular arc with center at the lens, whereas for a lens to object distance of 0.25m the curvature is much smaller.
The curvature of field causes of course problems with resolution, as the lens normally is designed to make good pictures of flat objects. The resolution can be effected by the size of the lens aperture as a small aperture has a greater depth of field than a big aperture. The great depth of field at for instance f/16 or f/22, can therefore almost take care of the curvature. Stopping down is therefore very important using a dome port.
Figure 4 below shows the same chart as in figures 1 and 2, now photographed using a dome port. The almost negligible distortion can be seen, as well as the decreased corner resolution. The decreased corner resolution is caused by the curvature of field only. Note that a large aperture of f/4 has been used to clearly show the effect. At f/16 the result is much better, and the effect had not been visible in pictures like these.
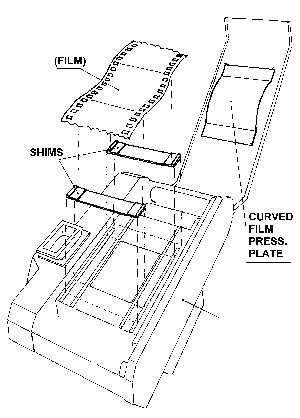
Once again, stopping down to smallest apertures of the lens is recommended. There are, however, other solutions to the problem. One involves modification of the film plane of your camera: a curved film plane, which matches the curvature of field. This is of course not a solution for everyone (not everyone dares to go into the expensive camera and make modifications), but it could be interesting to know, that a not completely unrealistic mechanical solution exists. Figure 5 shows the result of this solution. The increased corner resolution is clearly verified. Figure 6 shows how this mechanical modification of the film plane can be performed.
|
Figure 4 |
|
|

|
This is a picture of the same testchart taken under water
Lens: Sigma 2.8/28
Aperture: 4
Window: Dome with radius 78 mm
A slight barrel-shaped distortion is visible as well as a decreased resolution at corners |
|
Figure 5 |
|
|

|
This is a picture of the same testchart taken under water
Lens: Sigma 2.8/28
Aperture: 4
Window: Dome with radius 78 mm
Curved film plane
Mark the increased resolution at corners, compared to figure 4 |
The curved film plane should of course ideally have been spherical (as the virtual picture), and not only single-curved. A spherical shape is not possible, and a perfect result can therefore not be expected. As the curvature is along the longer side of the picture, the effect is however rather good.
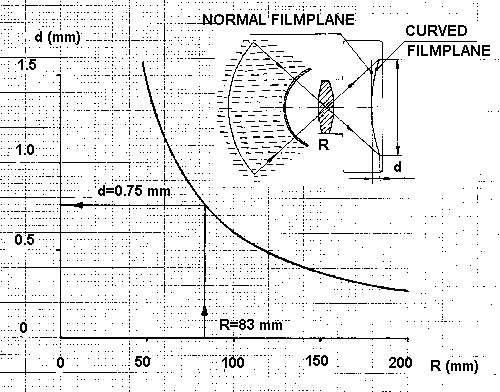
Figure 6.
Shims together with a curved film pressure plate are causing the film to adapt to the desired curved shape. The thickness of the shims and the curvature of the film pressure plate are given by
d for different dome radii R (the curve is valid for the 35mm film format only).
The mechanical solution of above is sometimes not possible or too difficult to perform. Unfortunately no simple optical solutions exist for lenses, which are designed to reproduce flat objects well. There are however fisheye lenses, which offer an extremely good solution of the problem with curvature of field, see The Superior Fisheye Lens and The Medium Size Format Under Water .
[1] McNeil, G.T.: "The Dome Port in Underwater Photography", Skin Diver Magazine, October 1970
Here is your path to the
frontpage .
Copyright © Leif Samuelsson 1998. All rights reserved.